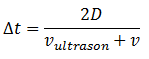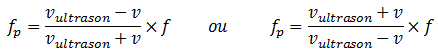Ex_TS_ondes-proprietes

Quelques propriétés des ondes : effet Doppler, diffraction, interférences :

Compétences exigées :

Ø Définir l'effet Doppler (conditions et observation). Citer et expliquer un exemple (simple) où l'effet Doppler est observé.

Ø Connaître la variation qualitative de la fréquence de l'onde reçue (estimer qualitativement le décalage Doppler de la fréquence) dans les 2 situations : la source et le récepteur se rapprochent, la source et le récepteur s'éloignent.

Ø Exploiter une expression (mathématique) donnée du décalage Doppler de la fréquence.

Ø Déterminer une vitesse en utilisant l'effet Doppler.

Ø Exploiter des données spectrales (fournies) pour illustrer l'utilisation de l'effet Doppler comme moyen d'investigation en astrophysique.

Ø Identifier, grâce à la longueur d'onde et aux dimensions de l'ouverture (ou de l'obstacle) rencontrée, les situations physiques où le phénomène de diffraction doit être pris en compte.

Ø Connaître et exploiter la relation θ = λ/a.

Ø Pratiquer une démarche expérimentale visant à étudier ou utiliser le phénomène de diffraction dans le cas des ondes lumineuses (notamment monochromatiques). Reconnaître une figure de diffraction ; délimiter sa tache centrale.

Ø Connaître les conditions générales pour que 2 ondes puissent interférer en un point de l'espace.

Ø Connaître et exploiter les conditions d'interférences constructives (déphasage nul) et destructives (opposition de phase) : conditions en termes de décalage temporel Δt et de différence de marche δ.

Ø Construire un montage expérimental permettant d'étudier le phénomène d'interférence dans le cas des ondes lumineuses (notamment monochromatiques). Identifier une frange brillante et une frange sombre ; mesurer précisément l'interfrange i (réaliser une photo de la figure d'interférence à l'aide d'une webcam ou d'un appareil photo numérique ; analyser l'intensité lumineuse d'une image avec le logiciel Regavi ou SalsaJ).

Ø Connaître et exploiter la relation approchée i = (λD)/a.

Exercices d'entraînement :

Exercice n°1 : L'effet Doppler

L'effet Doppler fut présenté par Christian Doppler en 1842 pour les ondes sonores puis par Hippolyte Fizeau pour les ondes électromagnétiques en 1848. Il a aujourd'hui de multiples applications.

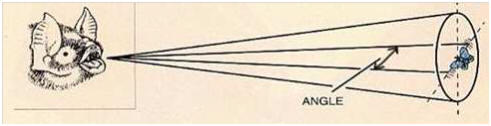
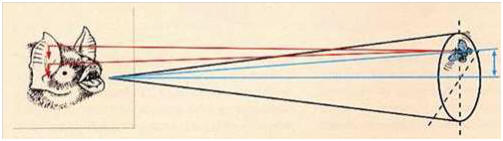
Un véhicule muni d’une sirène émet une onde sonore périodique, par exemple des « bips ». La durée qui s’écoule entre deux bips est la période temporelle T de l’onde. Lorsque le véhicule est immobile, la figure de gauche représente l’onde sonore se déplaçant à la célérité c = 340 m.s^-1 par rapport à un observateur lorsque le véhicule est immobile. Dans ce cas, la longueur d’onde perçue par le véhicule et celle perçue par l’observateur sont égales.

Lorsque le véhicule se déplace à la vitesse v en se rapprochant de l’observateur, l’onde sonore, se déplaçant à la même célérité c que précédemment, peut être représentée par la figure de droite.

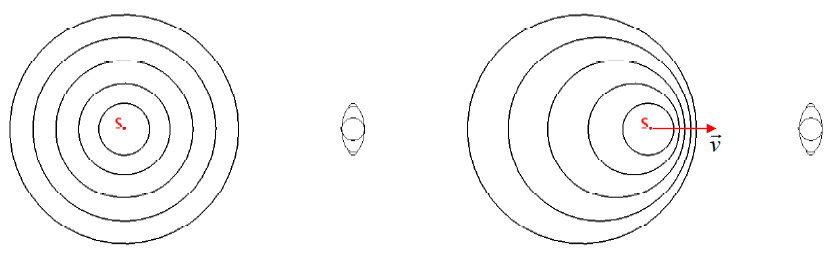
On note λ la longueur d’onde de l'onde perçue par l’observateur lorsque le véhicule est immobile, et λ' la longueur d’onde de l'onde perçue par l’observateur lorsque le véhicule se rapproche de lui. Pendant la durée T, le premier bip parcourt dans l’air la distance d = c.T, qui est donc égale à la longueur d’onde de l’onde sonore perçue par l’observateur lorsque le véhicule est immobile. Lorsque le véhicule émet le second bip, il a parcouru une distance d_v = v.T. Les deux bips sont donc maintenant séparés par une distance d’ = d – d_v.

1. Montrer en vous aidant du texte que λ' = λ – v.T.

2. Quelle est la relation générale liant la fréquence, la longueur d’onde et la célérité ?

3. En déduire que la fréquence du son perçu par l’observateur vaut f ' = (c.f)/(c-v).

4. Le son perçu par l’observateur est-il plus grave ou plus aigu que le son d’origine ? Justifier.

On suppose maintenant que le véhicule s’éloigne de l’observateur.

5. Quelle est la relation dans ce cas entre la fréquence f’’ du son perçu et la fréquence f du son d’origine ?

6. Le son perçu par l’observateur est-il plus grave ou plus aigu que le son d’origine ?

Exercice n°2 : Edwin Hubble et l'expansion de l'Univers

Document 1 : L'effet Doppler

L'effet Doppler (ou Doppler-Fizeau) traduit le décalage de longueur d'onde (ou de fréquence) perçu par un observateur lorsqu'une onde est reçue en provenance d'un émetteur en mouvement par rapport à la situation où ce même émetteur est immobile.

Il peut être montré que ce décalage est proportionnel à la vitesse de l'émetteur et dépend du sens du mouvement.

Document 2 : Résultats historiques de Edwin Hubble

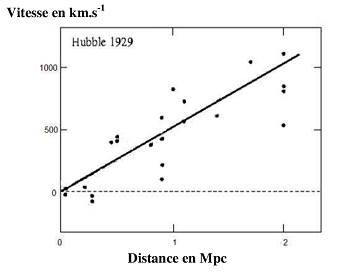
Dès 1929, Edwin Hubble a remarqué que la vitesse à laquelle semblaient s'éloigner les galaxies qu'il observait était proportionnelle à leur distance à la Terre. La constante de proportionnalité a ensuite été appelée "constante de Hubble". La figure ci-dessus indique les premiers résultats obtenus par Edwin Hubble en 1929, pour des galaxies très proches (distance inférieure à 2 Mpc*).

* Le mégaparsec noté Mpc est une unité de distance utilisée couramment en astronomie

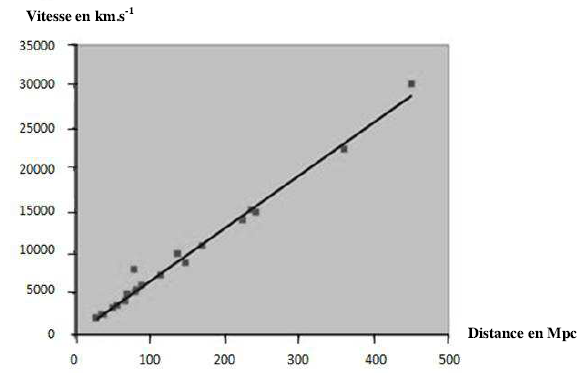
Document 3 : La loi de Hubble en 1996 (Vitesse des galaxies en fonction de leur distance à la Terre jusqu'à 500 Mpc)

1. Expliquer le « Schéma de l'effet Doppler » du document 1 (c'est une galaxie qui est représentée au centre du cercle le plus petit).

2. La galaxie NGC 3627 (voir document 1) s'éloigne-t-elle ou se rapproche-t-elle de la Terre ? Justifier clairement. la réponse.

3. Commenter la phrase « Edwin Hubble a remarqué que la vitesse à laquelle semblaient s'éloigner les galaxies qu'il observait était proportionnelle à leur distance à la Terre ».

4. La constante de proportionnalité dite « constante de Hubble » est notée en général H₀.

4.1. À partir du graphique du document 2, estimer la valeur de H₀ proposée par Edwin Hubble. On précisera l'unité associée à cette valeur.

En réalité des mesures plus récentes ont permis d'obtenir des mesures plus précises sur des galaxies plus éloignées (voir document 3).

4.2. Discuter de la validité de la loi de Hubble et comparer la valeur actuelle de H₀ à celle proposée par Edwin Hubble.

Exercice n°3 : Couche « antireflet »

On utilise un LASER, émettant une radiation de longueur d’onde dans le vide λ₀ = 650 nm, afin de réaliser des mesures à l’intérieur d’une cuve, dont les parois sont en verre d’indice de réfraction N = 1,5. Pour éviter les réflexions du faisceau LASER sur la face d’entrée du dispositif, on désire la recouvrir d’une couche « antireflet ».

L’objectif de cet exercice est de déterminer l’indice de réfraction n et l’épaisseur e de la couche (transparente) à déposer sur la cuve en verre pour annuler la réflexion de la lumière LASER en incidence normale (le faisceau incident est alors perpendiculaire à la surface de la cuve en verre).

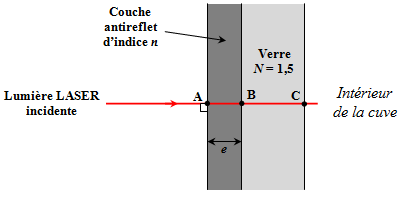
Une partie (notée 1) de la lumière LASER incidente représentée sur le schéma ci-dessus peut être directement réfléchie en A et revenir. Une autre partie (notée 2), qui pénètre plus profondément, peut être réfléchie en B avant de revenir en repassant par A.

1) a) Pourquoi peut-on avoir interférences entre les parties 1 et 2 de la lumière LASER ?

b) Pour supprimer le « reflet » en incidence normale, les interférences des parties 1 et 2 de la lumière LASER doivent-elles être constructives ou destructives ?

2) Pour supprimer complètement le « reflet » en incidence normale, il faut que les parties 1 et 2 de la lumière LASER aient la même intensité. Cette condition est réalisée lorsque . Combien vaut l’indice de réfraction n de la couche « antireflet » ?

3) Contrairement à la fréquence f, la longueur d’onde dépend du milieu traversé par la radiation. Montrez que l’expression de la longueur d’onde λ de la radiation LASER dans la couche « antireflet » est : λ₀/n. Donnez alors la valeur de λ.

4) Déterminez, à l’aide du schéma et en fonction de e, une expression de la différence de marche δ entre la partie 1 et la partie 2 de la lumière LASER (parties qui vont interférer).

5) a) Ecrivez la condition sur la différence de marche δ pour que l’on ait les interférences indiquées en réponse à la question 1)b).

b) Déduisez-en la plus petite valeur de l’épaisseur e de cette couche « antireflet ».

6) Au fur et à mesure des manipulations de la cuve par l’expérimentateur, des rayures peuvent apparaître sur la couche « antireflet ». Quel phénomène physique peut éventuellement se produire ? Que peut-on alors observer et dans quelle(s) condition(s) ?

Dans un milieu transparent quelconque, la longueur d’onde λ (m) vaut : v/f où f est la fréquence en Hz et v est la célérité de la lumière dans le milieu en m/s.

L'indice de réfraction n d'un milieu transparent est défini par : n = c/v où c est la célérité de la lumière dans le vide (m/s)

Exercice n°4 : L'écholocation chez les chauves-souris (exercice récapitulatif sur les ondes)

Les chauves-souris se déplacent et chassent dans l’obscurité grâce à un système très perfectionné d'écholocation : elles émettent des signaux ultrasonores et en exploitent les échos. On se propose d'étudier quelques aspects de cette technique.

L’amplitude de l’écho reçu donne une information sur la taille de la proie :

Pour estimer la distance à une proie ou à un obstacle, les organes sensoriels de la chauve-souris enregistrent le retard de l'écho par rapport à l'émission du signal.

La différence de réception de l’écho dans les deux oreilles (d’une chauve-souris) détermine l’azimut (positionnement horizontal) de la proie :

La chauve-souris perçoit sa vitesse relative par rapport à un obstacle ou à une proie grâce au décalage de fréquence du signal réfléchi dû à l'effet Doppler.

Les battements d'ailes d'un insecte produisent un décalage des fréquences par effet Doppler oscillant, qui se superpose au décalage général engendré par les obstacles fixes environnants. Chez certaines espèces, pour faciliter la détection de ces oscillations, il existe un système de compensation : ces espèces modifient la fréquence d'émission pour que la fréquence du signal réfléchi par les obstacles fixes soit ramenée à une fréquence de référence, celle qui est émise lorsque l'animal est immobile, et pour laquelle leur sensibilité est maximale.

Donnée : La célérité des ultrasons dans l'air est : v_ultrason = v_son = 340 m.s^-1.

1.1. D’après le document, l’amplitude de l’écho reçu permet aux chauves-souris d’estimer la taille d’une proie, néanmoins cela s’avère très difficile voire impossible si la proie (potentielle) est trop petite. Quel phénomène, caractéristique des ondes, est responsable de cette limite ?

1.2. Déterminez, en expliquant, l’ordre de grandeur de la taille minimale d'un insecte détectable avec un signal ultrasonore de fréquence 30 kHz.

On considère dans cette partie, une chauve-souris qui se dirige vers un mur perpendiculairement à celui-ci, à la vitesse v = 6,0 m.s^-1. Un signal ultrasonore émis, lorsqu’elle se trouve à la distance D = 3,0 m du mur, produit un écho qu'elle perçoit après une durée notée Δt.

2.1. Donner, en fonction de v et Δt, l'expression littérale de la distance d parcourue par la chauve-souris pendant la durée de l'écho Δt.

2.2. Déterminer l'expression littérale de la distance de propagation du signal ultrasonore d_ultrason pendant son aller-retour en fonction de D, v et Δt.

2.3. Montrer alors que l'expression de la durée de l'écho Δt est celle indiquée ci-dessous, puis calculer cette durée Δt.

2.4. Si on néglige le déplacement de la chauve-souris pendant l’aller-retour du signal ultrasonore, que devient l'expression précédente de Δt ? Calculer la nouvelle valeur de la durée de l’écho. Peut-on, à votre avis, négliger le déplacement de la chauve-souris dans le calcul de Δt ?

3.1. Rappeler en quoi consiste l'effet Doppler et illustrer la réponse par un exemple simple du quotidien.

3.2. Lorsqu'une chauve-souris se dirige vers un mur, l'écho perçu ensuite a-t-il une fréquence plus grande ou plus faible que celle du signal ultrasonore émis ?

3.3. On propose deux expressions pour la relation entre la fréquence perçue f_p et la fréquence d'émission f pour une chauve-souris se dirigeant vers un mur perpendiculairement à celui-ci avec la vitesse v :

4.1. Dans le document, il est question de « différence de réception de l’écho dans les deux oreilles ». Citez une différence entre les deux signaux reçus (un par oreille) qui pourraient expliquer la détermination du positionnement horizontal, c’est-à-dire pour simplifier, le fait que la proie se trouve plutôt à gauche ou à droite de la chauve-souris ?

4.2. La détermination du positionnement vertical est, entre autres, basé sur le phénomène d’interférence comme pour l’être humain. A quelles conditions deux ondes peuvent-elles interférer ? Indiquez sur le schéma de l’oreille humaine ci-dessous, en quel point les deux ondes reçues interfèrent.

4.3. Le fait que l’interférence puisse être constructive ou destructive dépend de la différence de marche δ. Indiquez δ sur le schéma de l’oreille humaine (ci-dessous).

Supposons δ = 1,7 cm pour une oreille humaine. Déterminez, dans ce cas, la plus petite valeur de fréquence pour que l’on ait une interférence destructive (cette valeur correspond à un « décrochage fréquentiel » ou « trou » qui varie suivant la taille des oreilles et l’orientation de la source sonore).

En arrivant en A et A', les deux ondes ci-contre ont parcouru la même distance dans l'air (depuis une source sonore).

Exercice n°4 : Le Compact-Disc (interférences et caractéristiques des ondes)

À partir du début des années 1980, le disque audio (CD) a supplanté les vinyles en raison d’une grande facilité d’utilisation et de la quantité d’information stockable.

Les documents nécessaires à la résolution sont regroupés en fin d’énoncé.

1.1. Montrez que la surface « utile » S du CD, correspondant à la surface grisée (document 1), s’exprime par : S = π.(R₂² – R₁²).

1.2. On peut estimer la longueur L de la piste par l’expression L ≈ S/a où a est le pas de la spirale. Évaluez la longueur de la piste de ce CD.

Lorsque le spot laser se réfléchit autour d’une alvéole, il y a interférences entre la partie de l’onde qui se réfléchit sur le plat et celle qui se réfléchit sur le creux.

1.4.1. Déterminez la différence de parcours entre l’onde qui se réfléchit sur un creux et celle qui se réfléchit sur un plat.

1.4.2. Ce parcours ayant lieu dans le polycarbonate, déterminez le retard de l’onde réfléchie dans un creux par rapport à l’onde réfléchie sur un plat au niveau du capteur.

1.4.4. Déduisez-en le type d’interférences (constructives ou destructives) entre l’onde réfléchie par un creux et celle réfléchie par un plat au niveau du capteur.

1.4.5. Dans ce cas, le signal reçu par le capteur est-il maximal ou minimal ? Commentez.