Les forces et les lois de Newton :
Compétences exigées sur les forces :
Ø
Identifier et
représenter par des forces les actions mécaniques qui s’exercent sur un
solide (2nde).
Ø
Schématiser des
forces en utilisant une échelle adaptée (2nde).
Ø
Connaître les
expressions littérales des valeurs du poids
(collège), de la poussée d’Archimède
et de la force
de rappel d’un ressort.
Ø
Appliquer
correctement le principe d’inertie (2nde).
Ø
Projeter des
forces sur des axes adaptés ; en
déduire les relations entre les composantes des forces afin de résoudre un
problème de physique.
Ø
Réaliser un graphique complet et
modéliser par un tracé adapté les points expérimentaux (2nde).
Ø Interpréter qualitativement les variations d'une courbe et déterminer, lorsque le tracé est linéaire, le coefficient directeur et l'équation de la droite (2nde).
Compétences exigées sur les lois de Newton :
Ø
Tracer
des vecteurs variation de vitesse (pour le centre d’inertie).
Ø
Connaître
les 3 lois de Newton. Appliquer
ces lois dans des situations adéquats.
Ø
Savoir
que les deux premières lois ne sont applicables que pour le centre d’inertie
G et dans des référentiels dits galiléens comme le référentiel terrestre.
Ø
Rappel :
projeter des forces sur des axes adaptés afin de résoudre un problème de
physique.
![]() Exercices d'entraînement :
Exercices d'entraînement :
Exercice n°1 : Etude d'un pendule (Chap 3 et chap 1 pour la dernière question)
Un pendule, servant à des expériences d'électrisation, est formé d'une boule métallique d'aluminium et d'un fil relié à une potence. On se propose d'étudier le système formé par la boule. Initialement, celle-ci est en équilibre, retenu par le fil vertical exerçant une tension de valeur T = 0,015 N.
1) Faîtes l'inventaire des forces qui s'exercent sur la boule.
2) Déterminez toutes les caractéristiques de ces vecteurs force.
3) Calculez la masse m de la boule.
On approche maintenant de la boule : une règle en PVC électriquement chargée. La boule est attirée, puis elle se maintient à l'équilibre retenu par le fil exerçant cette fois-ci une tension de valeur T' = 0,019 N. On a la situation suivante :
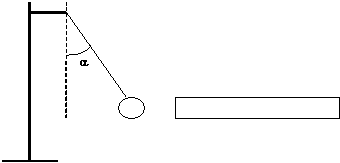
4) Faîtes l'inventaire des forces s'appliquant sur la boule.
5) Faîtes (sans tenir compte de l'échelle) un schéma où seront représentées les forces.
6) Quelle relation a-t-on entre les vecteurs force ? Justifiez.
7) Projetez cette relation sur des axes Ox et Oy d'un repère adapté que vous choisirez. Déterminez ensuite la valeur de a, puis celle de la force électrique notée F.
8) Sachant que la boule porte une charge qb = 1,00´10-9 C et la règle une charge qrègle = - 3,50 nC, calculez la distance d entre la boule et la règle.
Données : L’intensité de la pesanteur g vaut 10 N.kg-1 ; k = 9,0´10-9 SI
Exercice n°2 : un liquide inconnu (Chap 3)
On accroche une boule métallique de rayon r = 2,0 cm et de masse m = 264 g au bout d'un ressort suspendu verticalement à une potence. Il s'agit d'un ressort de raideur k = 70 N.m-1 et de longueur à vide L0 = 25 mm.
On plonge entièrement la boule (accrochée au ressort) dans une cuve contenant un liquide inconnu de densité notée d. La longueur L du ressort est alors de 5,4 cm.
1) Déterminez la valeur du poids de la boule et celle de la force de rappel du ressort.
2) Identifiez la 3ème force s'exerçant sur la boule. Déterminez alors sa valeur.
3) Représentez clairement les forces sur un schéma. On indiquera l'échelle choisie.
4) Calculez le volume V de la boule. Déterminez ensuite la densité du liquide notée d.
Données : L’intensité de la pesanteur g vaut 9,8 N.kg-1 ; ρeau= 1,0×103 kg.m-3 ; l'expression du volume d'une boule est nécessaire.
Exercice n°3 : Mouvement d'une luge sur une piste enneigée (Chaps 3 et 4)
Jean pousse une luge (avec son fils dedans) sur une distance de 3,0 m sur la partie horizontale de la piste enneigée afin de lui donner assez de vitesse pour atteindre la pente (voir ci-dessous ; le schéma n'est pas réaliste...). La masse du système {luge + fils}est de 30 kg et le référentiel d'étude sera le référentiel terrestre. L’intensité de la pesanteur g vaut 9,8 N.kg-1.
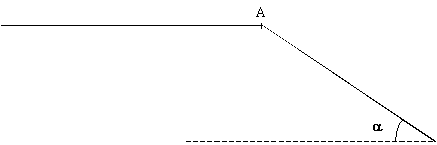
1) Que pouvez-vous dire de la force (supposée horizontale) exercée par Jean sur la luge et de la force exercée par la luge sur Jean pendant la phase de poussée ? Justifiez.
Etude de la luge avant le point A :
Dans cette partie, la luge n'est plus poussée et les frottements entre la luge et la piste ne sont pas négligeables, contrairement à ceux dus à l'air.
2) Faîtes le bilan des forces s'exerçant sur la luge et représentez-les sur un schéma (sans tenir compte de l'échelle).
3) a) Démontrez en appliquant la 2ème loi de Newton que le vecteur variation de vitesse du centre d'inertie G du système est horizontal et dirigé vers la gauche.
b) Que peut-on alors dire du mouvement du centre d'inertie G sur cette partie de la piste ?
Etude de la luge après le point A :
On suppose que la luge réussit à atteindre la pente. Sur cette piste pentue de a =10°, la luge a (du moins au début...) un mouvement rectiligne et accéléré. On suppose qu'elle est toujours soumise aux frottements de la piste considérés comme constants.
4) a) Représentez clairement les forces s'exerçant sur le système sur un autre schéma (sans tenir compte de l'échelle).
b) Projetez les forces parallèlement (axe Ox) et perpendiculairement (axe Oy) à la pente.
c) Déterminez (en expliquant) la valeur RN de la réaction normale de la piste sur le système.
d) Quelle relation a-t-on forcément entre les projetés des forces sur l'axe Ox pour que le type de mouvement soit respecté ? Justifiez.
5) Le mouvement de la luge devient en réalité uniforme au bout d'un certain temps. Le choix des forces vous paraît-il alors judicieux ? Expliquez.
Exercice n°4 : Expérience avec un mobile autoporteur (Chaps 2, 3 et 4)
On
a enregistré le mouvement du centre d'inertie M d'un mobile autoporteur (sur
une table à coussin d'air) sur le document ci-dessous avec un intervalle de
temps τ
1) Il y a apparemment deux phases distinctes dans le mouvement.
a) Donnez sous la forme MiMj
les deux parties correspondantes à ces
deux phases. On les notera (1) et (2) par la suite.
b) Pour chacune des phases, donnez deux qualificatifs au mouvement et précisez si le vecteur vitesse du point M est constant.
2) Calculez la vitesse du point M pour la phase (1) puis pour la phase (2) à l'aide de l'enregistrement en m.s-1 et en km.h-1.
3) Pour quelle phase la notion de vitesse angulaire a-t-elle un sens ? Donnez la définition de la vitesse angulaire pour cette phase à l'aide de notations claires.
Etude
de la phase (1) :
4) A quoi peut correspondre le point (fixe) O pour cette phase ?
5)
Construisez le vecteur variation de vitesse pour la position M5. On
laissera et on identifiera tous les tracés nécessaires sur le document. On
prendra comme échelle des vitesses :
6) Que peut-on affirmer concernant la phase (1) à l'aide de la 2ème loi de Newton et de la réponse à la question précédente ?
7) a) S'agissant du mouvement d'un mobile sur une table à coussin d'air, quelles sont les 2 forces que l'on doit obligatoirement considérées ?
b) On considère qu'il n'y a pas de frottement entre le mobile et la table considérée comme horizontale. Peut-on uniquement considérer les 2 forces précédentes pour cette phase? Pourquoi ?
c) Etant données les réponses aux questions 4) et 7)b), à quelle autre force a-t-on pu soumettre le mobile au cours de cette phase ? Comment a-t-on pu s'y prendre pour l'exercer ?
Passage de la phase (1) à la phase (2) :
8) Quelle loi de Newton peut-on appliquer dans la phase (2) ? Justifiez.
La laborantine se souvient qu'elle n'avait pas fait très attention à cet enregistrement, car il y avait eu un problème au cours de l'expérience. Néanmoins, elle ne se souvient plus de quel problème il s'agissait... Etant donnée la différence de mouvement entre les deux phases, le problème a du surgir lors du passage de la phase (1) à la phase (2).
9) Que s'est-il produit au cours de l'expérience et qui explique le changement de mouvement entre les deux phases ? On pourra s'aider de la fin de l'étude de la phase (1).